Speculation aside, your assistant, Johannes Kepler now has access to your lab and notes, and man does he go to town. Within a couple of decades of Tycho's death he had worked out 3 laws of planetary motion:
1. Planets orbit the sun in ellipses with the sun at one focus
Some maths now. An ellipse, in layman's terms, is a squished circle. If that's good enough for you then just go ahead to the second law now. See you there in a bit.
Mathematically, an ellipse is a set of points that satisfies the equation:
- x2⁄a2 + y2⁄b2 = 1
Ellipses have an eccentricity 'e', which is basically to what degree they are squished.
- e ≡ √1 - b2⁄a2
Do please ignore the godawful overline job there. That's meant to be all square rooted. But as you can see, if a=b then eccentricity is 0, and you get a circle. On the other hand as e approaches 1, through oversized a or undersized b, then we're more or less getting a line.
Here is the eccentricity of the planets we've discovered so far:
Earth - 0.017
Venus - 0.007
Mars - 0.093
Jupiter - 0.048
Saturn - 0.056
Mercury - 0.206
Clearly most of our neighbours are fairly normal. Venus is practically Ned Flanders. Mercury on the other hand is down right ovular in it's travels, and this was something that had baffled astronomers who had previously believed that everything moved around in nice polite circles.
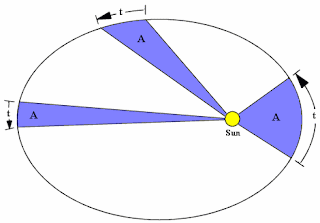
2. "Equal area" is swept out in "equal time".
This one is simple enough. See the orbit below?
During a value of time t, wherever the planet is in the orbit, the area cleared between it and the star will be area A. Next.
3. The relationship between period p and distance from the star is:
Earth - 0.017
Venus - 0.007
Mars - 0.093
Jupiter - 0.048
Saturn - 0.056
Mercury - 0.206
Clearly most of our neighbours are fairly normal. Venus is practically Ned Flanders. Mercury on the other hand is down right ovular in it's travels, and this was something that had baffled astronomers who had previously believed that everything moved around in nice polite circles.
 |
| This was the equivalent of not thanking someone after they hold a door open for you. |
This one is simple enough. See the orbit below?
During a value of time t, wherever the planet is in the orbit, the area cleared between it and the star will be area A. Next.
3. The relationship between period p and distance from the star is:
a3 = p2
Now I've already said a lot on the subject of Galileo and his life including the fact that he didn't invent the telescope, as is so often claimed. Thus I shall not dwell for too long on such matters. I did mention that he made a number of discoveries with his telescope however, and I shall briefly expand upon a few of them.
There's not much more to say on that matter so have some data on it.
Ah but I wish you could make decent tables in Blogger.
- He discovered mountains on our own moon.
- He had a good look at the celestial Thursday that is Jupiter, and observed that it had four moons of it's own; Io, Europa, Ganymede, and Callisto. These are known as, understandably, the Galilean moons.
- He worked out that the moons satisfy a "Kepler-like orbit", that is to say that the cube of the distance between them and Jupiter is proportional to the square of the orbital period.
All in all everything he discovered kinda fought against the idea of geocentricism. After that, well, like I say, I've gone into it already. Let's briefly move onto someone New...ton.
Sorry. Anyway, Kepler's laws were pretty observation based. They worked, absolutely, but the maths behind it was lacking. So the story goes, having had a crack at it himself this bloke called Christopher Wren made what is known in the business as a Scientific Wager, offering 40 shillings to anyone who could deduce Kepler's Laws from the inverse square law. Alas, while Newton had a stab at it, by the time he had finished he was too late. His only consolation was that his work grew into one of, if not the most important pieces of work in science. The 40 shillings would have been nice though.





0 comments:
Post a Comment